Implémentation des graphes

Il existe de multiples manières de représenter un graphe, selon la nature du graphe mais aussi selon la nature des opérations que l'on souhaite effectuer sur ce graphe. Quelque soit le choix retenu, on souhaite pouvoir :

• utiliser des opérations de construction du graphe. Il faut pouvoir ajouter/supprimer des sommets, des arcs…
• utiliser des opérations de parcours du graphe : parcourir la liste des sommets, des arcs, ou bien des arcs issus d'un sommet donné…

On s'intéresse dans ce TP aux implémentations des graphes orientés.

Matrices d'adjacence

Les sommets du graphe sont les nombres \(0, 1, \ldots, n - 1\), pour un certain entier \(n\in \mathbb{N}\). On représente le graphe à l'aide d'une matrice adj de taille \(n \times n\) (un tableau constitué de \(n\) lignes et \(n\) colonnes). Il existe un arc entre les sommets \(i\) et \(j\) du graphe si et seulement si adj[i][j] vaut True.

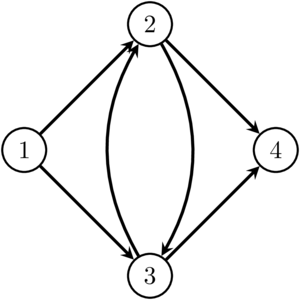
Matrice d'adjacence adj de \(G_1\).

On donne ci-dessous le code python du constructeur de la classe Graphe.

###

Lancer Télécharger Téléverser Recharger Sauvegarder

class Graphe:bksl-nl """ Un graphe représenté par une matrice d'adjacence.bksl-nl Les sommets sont les nombres 0, 1, ..., n - 1. """bksl-nl def py-undpy-undinitpy-undpy-und(self, n):bksl-nl self.n = nbksl-nl self.adj = [[False]py-strn for py-und in range(n)]bksl-nlbksl-nl def ajouterpy-undsommet(self):bksl-nl """ Graphe -> Nonetypebksl-nl Ajoute un sommet au graphe """bksl-nl passbksl-nlbksl-nl def ajouterpy-undarc(self, source, destination):bksl-nl """ Graphe, int, int -> intbksl-nl Ajoute l'arc source -> destination """bksl-nl passbksl-nlbksl-nl def supprimerpy-undsommet(self, i):bksl-nl """ Graphe, int -> Nonetypebksl-nl Supprime le sommet i du graphe. Les sommets j > i sont renommés en j - 1. """bksl-nl passbksl-nlbksl-nl def supprimerpy-undarc(self, source, destination):bksl-nl """ Graphe, int, int -> Nonetypebksl-nl Supprime l'arc source -> destination """bksl-nl passbksl-nlbksl-nl def estpy-undvoisin(self, source, destination):bksl-nl """ Graphe, int, int -> boolbksl-nl Détermine si source et destination sont voisins """bksl-nl passbksl-nlbksl-nl def sommets(self):bksl-nl """ Graphe -> [int]bksl-nl Renvoie la liste des sommets du graphe self """bksl-nl passbksl-nlbksl-nl def voisins(self, sommet):bksl-nl """ Graphe, int -> [int]bksl-nl Renvoie la liste des voisins de sommet """bksl-nl passbksl-nlbksl-nl def listepy-undarcs(self):bksl-nl """ Graphe -> [(int, int)]bksl-nl Renvoie la liste des arcs du graphe """bksl-nl passbksl-nlbksl-nl def ordre(self):bksl-nl """ Graphe -> intbksl-nl Renvoie l'ordre du graphe """bksl-nl passbksl-nlbksl-nl def taille(self):bksl-nl """ Graphe -> intbksl-nl Renvoie la taille du graphe """bksl-nl passbksl-nlbksl-nl def decrire(self):bksl-nl """ Graphe -> Nonetypebksl-nl Affiche une description du graphe self """bksl-nl passbksl-nlbksl-nl

1. 1. Initialiser une variable g1 de type Graphe, représentant un graphe constitué des 4 somments \(0\), \(1\), \(2\), et \(3\). Initialement, aucun arc n'est présent dans le graphe g1.

   2. Écrire une méthode sommets de la classe Graphe qui étant donné un graphe self renvoie la liste des sommets qui le constituent.

      def sommets(self):
          """ Graphe -> [int]
          Renvoie la liste des sommets du graphe self """
          pass
      

      print(g1.sommets())          
      

      [0, 1, 2, 3]
      

2. 1. Écrire une méthode ajouter_arc de la classe Graphe qui étant donné deux sommets source et destination du graphe self ajoute l'arc source \(\to\) destination au graphe self.

      def ajouter_arc(self, source, destination):
          """ Graphe, int, int -> None
          Ajoute l'arc source -> destination """
          pass
      

   2. À l'aide de la méthode ajouter_arcs, construire le graphe g1 de l'énoncé.

      for row in g1.adj:
          print(row)          
      

      [False, True, False, True]
      [False, False, False, True]
      [False, True, False, False]
      [False, False, True, False]
      

   3. Écrire une méthode est_voisin de la classe Graphe qui étant donné deux sommets source et destination du graphe self renvoie True si et seulement si il existe un arc reliant source à destination dans le graphe self.

      def est_voisin(self, source, destination):
          """ Graphe, int, int -> bool
          Détermine si source et destination sont voisins """
          pass
      

      print(g1.est_voisin(0, 1))          
      print(g1.est_voisin(1, 0))          
      

      True
      False
      

3. 1. Écrire une méthode voisins de la classe Graphe qui étant donné un sommet du graphe self renvoie la liste des voisins de sommet.

      def voisins(self, sommet):
          """ Graphe, int -> [int]
          Renvoie la liste des voisins de sommet """
          pass
      

      print(g1.voisins(0))          
      print(g1.voisins(1))          
      

      [1, 3]
      [3]
      

   2. Écrire une méthode liste_arcs de la classe Graphe qui renvoie la liste des couples (source, destination) correspondants à des arcs du graphe self.

      def liste_arcs(self):
          """ Graphe -> [(int, int)]
          Renvoie la liste des arcs du graphe """
          pass
      

      print(g1.liste_arcs())          
      

      [(0, 1), (0, 3), (1, 3), (2, 1), (3, 2)]
      

4. 1. Écrire une méthode ordre de la classe Graphe qui renvoie l'ordre du graphe.

      Rappel. L'ordre d'un graphe est le nombre de sommets qui composent le graphe.

      def ordre(self):
          """ Graphe -> int
          Renvoie l'ordre du graphe  """
          pass
      

      print(g1.ordre())         
      

      4
      

   2. Écrire une méthode taille de la classe Graphe qui renvoie la taille du graphe.

      Rappel. La taille d'un graphe est le nombre d'arêtes qui composent le graphe.

      def taille(self):
          """ Graphe -> int
          Renvoie la taille du graphe """
          pass
      

      print(g1.taille())          
      

      5
      

   3. Écrire une méthode decrire qui affiche les informations du graphe self sur le modèle donné ci-dessous.

      def decrire(self):
          """ Graphe -> None
          Affiche une description du graphe self """
          pass
      

      g1.decrire()          
      

      Graphe d'ordre 4 et de taille 5
      Sommet 0 -> 1 3
      Sommet 1 -> 3
      Sommet 2 -> 1
      Sommet 3 -> 2
      

5. 1. Écrire une méthode ajouter_sommet de la classe Graphe qui ajoute un sommet au graphe. Ainsi, si le graphe g est constitué de \(n\) sommets, alors après l'application de la méthode ajouter_sommet le graphe est constitué de \(n + 1\) sommets (le sommet ajouté est \(n\)) : la méthode ajouter_sommet modifiera à la fois l'attribut n et l'attribut adj du graphe self. Aucun arc ne sera ajouté par cette méthode.

      def ajouter_sommet(self):
          """ Graphe -> None
          Ajoute un sommet au graphe """
          pass
      

      g1.ajouter_sommet()          
      g1.decrire()
      

      Graphe d'ordre 5 et de taille 5
      Sommet 0 -> 1 3
      Sommet 1 -> 3
      Sommet 2 -> 1
      Sommet 3 -> 2
      Sommet 4 ->
      

   2. Écrire une méthode supprimer_arc de la classe Graphe qui supprime (si présent) l'arc reliant source à destination dans le graphe self. Cette méthode ne produira pas d'erreur dans le cas où le graphe ne contient pas l'arc (source) \(\to\) (destination).

      def supprimer_arc(self, source, destination):
          """ Graphe, int, int -> None
          Supprime l'arc source -> destination """
          pass
      

   3. Écrire une méthode supprimer_sommet de la classe Graphe qui supprime le sommet i du graphe self. La méthode supprimer_sommet modifiera l'attribut n et l'attribut adj. Si \(j > i\) est un sommet du graphe, alors son numéro sera \(j - 1\) après application de la méthode supprimer_sommet, les sommets \(j < i\) conserveront le même numéro.

      def supprimer_sommet(self, i):
          """ Graphe, int -> None
          Supprime le sommet i du graphe. Les sommets j > i sont renommés en j - 1. """
          pass
      

      g1.supprimer_sommet(2)
      g1.decrire()
      

      Graphe d'ordre 4 et de taille 3
      Sommet 0 -> 1 2
      Sommet 1 -> 2
      Sommet 2 -> 
      Sommet 3 ->
      

Dictionnaire d'adjacence

Les sommets du graphe sont quelconques (des nombres, non forcément consécutifs, des lettres, des mots, etc). On représente un graphe à l'aide d'un dictionnaire d'adjacence, noté adj. Si \(G = (S, A)\), alors les clés du dictionnaire adj seront les éléments de \(S\). La valeur associée à la clé source sera la liste des sommets destination de telles que (source, destination) \(\in A\).

Par exemple si \(G_2\) est le graphe :

Alors le dictionnaire correspondant est :

adj = {'A': ['B', 'C', 'D'],
       'B': ['D'],
       'C': ['A', 'D'],
       'D': ['E'],
       'E': ['F'],
       'F': ['E']}    

On donne ci-dessous le code python du constructeur de la classe Graphe.

###

Lancer Télécharger Téléverser Recharger Sauvegarder

class Graphe:bksl-nl """ Un graphe représenté par un dictionnaire d'adjacence. """bksl-nl def py-undpy-undinitpy-undpy-und(self, n):bksl-nl self.n = nbksl-nl self.adj = [[False]py-strn for py-und in range(n)]bksl-nlbksl-nl def ajouterpy-undsommet(self, s):bksl-nl """ Graphe, str -> Nonetypebksl-nl Ajoute le sommet s au graphe self """bksl-nl passbksl-nlbksl-nl def ajouterpy-undarc(self, source, destination):bksl-nl """ Graphe, str, str -> Nonetypebksl-nl Ajoute l'arc source -> destination au graphe self """bksl-nl passbksl-nlbksl-nl

Toutes les questions de cette partie concernent cette classe Graphe, qui sera écrite dans un nouveau fichier. Les sommets seront ici des chaînes de caractère.

1. Donner la représentation sous forme de dictionnaire des graphes orientés de la fiche "Exercices de compréhension".

2. 1. Initialiser une variable g2 de type Graphe représentant un graphe initialement vide.

   2. Écrire une méthode ajouter_sommet qui ajoute un sommet s au graphe self. Initialement, aucun arc ne sort du sommet ajouté. Si le sommet est déjà présent dans le graphe, alors cette méthode ne fait rien.

      def ajouter_sommet(self, s):
          """ Graphe, str -> None
          Ajoute le sommet s au graphe self
          Ne fait rien si le sommet est déjà présent dans le graphe """
          pass
      

   3. Écrire une méthode ajouter_arc de la classe Graphe qui étant donné deux sommets source et destination du graphe self ajoute l'arc source \(\to\) destination au graphe self.

      def ajouter_arc(self, source, destination):
          """ Graphe, str, str -> None
          Ajoute l'arc source -> destination au graphe self """
          pass
      

   4. À l'aide des méthodes ajouter_sommet et ajouter_arc, construire le graphe g2 de l'énoncé.

      print(g2.adj) 
      

      {'A': ['B', 'C', 'D'], 'B': ['D'], 'C': ['A', 'D'], 'D': ['E'], 'E': ['F'], 'F': ['E']}
      

3. Écrire les méthodes est_voisin, sommets, voisins, liste_arcs, ordre, taille, decrire, supprimer_arc, supprimer_sommet (dans cet ordre) de la classe Graphe (ainsi que leur signature et leur documentation). VOUS TESTEREZ VOS MÉTHODES.

   g2.decrire()       
   

   Graphe d'ordre 6 et de taille 9
   Sommet A -> B C D
   Sommet B -> D
   Sommet C -> A D
   Sommet D -> E
   Sommet E -> F
   Sommet F -> E
   

   g2.supprimer_sommet('C')       
   g2.decrire()       
   

   Graphe d'ordre 5 et de taille 6
   Sommet A -> B D
   Sommet B -> D
   Sommet D -> E
   Sommet E -> F
   Sommet F -> E
   

4. Écrire la méthode predecesseurs de la classe Graphe qui étant donné un graphe self et un sommet destination renvoie la liste des prédécesseurs de source.

   Attention. Dans l'exemple, le sommet 'C' a été supprimé lors des exemples de la question précédente.

   def predecesseurs(self, destination):
       """ Graphe, str -> [str]
       Renvoie la liste des prédécesseurs de u """
       pass
   

   print(g2.predecesseurs('D'))
   

   ['A', 'B']
   

Chemins dans les graphes acycliques

Un graphe orienté est dit acyclique lorsqu'il n'existe aucun cycle dans le graphe. On parle de DAG pour Directed Acyclic Graph. Par exemple, dans la feuille "Exercices de compréhension", \(G_3\) est un graphe orienté acyclique. \(G_4\) n'est pas un graphe orienté acyclique : par exemple \(c \rightarrow e \rightarrow c\) est un cycle.

Écrire une fonction récursive chemin qui prend en argument un graphe g acyclique, deux sommets u et v du graphe et qui renvoie True s'il existe un chemin de u à v, False sinon.

1. Pourquoi est-il important de supposer que g est acyclique ? Que risque-t-il de se passer si on exécute chemin(g, u v) si g possède un cycle ?
2. Pouvez-vous modifier votre fonction pour que la fonction chemin renvoie :
   • la liste des sommets du chemin dans le cas où il existe un chemin entre u et v. Le premier élément de la liste doit être u, le dernier élément de la liste doit être v.
   • la liste vide si il n'existe pas de chemin reliant u à v.

Rappels

Si l est un objet de type list, i un indice compatible avec la taille de la liste, et e1 un élément présent dans la liste l, e2 un élément non présent dans la liste l :

• l.copy() renvoie une copie indépendante de l
• e1 in l s'évalue à True ; e2 in l s'évalue à False
• l.pop() supprime le dernier élément de la liste, l.pop(i) supprime l'élément d'indice i de la liste.
• l.remove(e1) supprime la première occurrence de e1 dans l ; l.remove(e2) soulève une erreur
• l.append(e2) ajoute l'élément e2 à la fin de la liste ; l.insert(i, e2) insère l'élément e2 à l'indice i.
• enumerate(l) renvoie la liste [(i, l[i]) for i in range(len(l))]

Si d est un objet de type dict, k1 une clé présente dans le dictionnaire, v1 la valeur associée à la clé k1, k2 une clé non présente dans le dictionnaire :

• d[k1] renvoie v1 ; d[k2] soulève une erreur ; d.get(k1) renvoie v1, d.get(k2) renvoie None ;
• k1 in d s'évalue à True ; k2 in d s'évalue à False
• d.pop(k1) supprime k1 de d et renvoie v1 ; d.pop(k2) soulève une erreur ;
• d.setdefault(k1, "valeur par defaut") ne fait rien car k1 est déjà présent dans le dictionnaire, d.setdefault(k2, "valeur par défaut") associe à k2 la valeur "valeur par défaut"
• d.keys() renvoie la liste des clés du dictionnaire ; d.values() renvoie la liste des valeurs du dictionnaire ; d.items() renvoie la liste des couples (clé, valeur) du dictionnaire ;